 |
 |
- Search
| Korean J Fam Med > Volume 38(5); 2017 > Article |
Abstract
Background
Methods
Results
References
Figure 1
The concordance of estimated LDL-C compared to cutoffs of NCEP-ATP III guideline. LDL-C, low-density lipoprotein cholesterol; NCEP-ATP III, National Cholesterol Education Program Adult Treatment Panel III; LDL-CF, estimated LDL-C level by Friedewald's equation; LDL-CH, estimated LDL-C level by Hatta's equation; LDL-CP, estimated LDL-C level by Puaviali's equation; LDL-CM, estimated LDL-C level by Martin's equation.
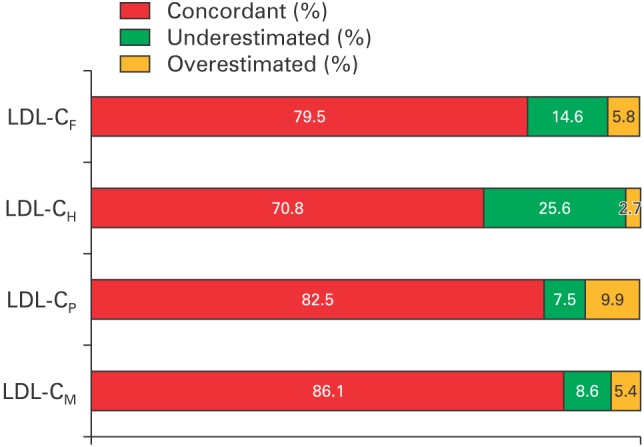
Figure 2
Proportions of percentage difference below 5% and 10% between directly measured and estimated LDL-C. All data are presented as %. LDL-C, low-density lipoprotein cholesterol; LDL-CF, estimated LDL-C level by Friedewald's equation; LDL-CH, estimated LDL-C level by Hatta's equation; LDL-CP, estimated LDL-C level by Puaviali's equation; LDL-CM, estimated LDL-C level by Martin's equation; Delta%, percentage difference between directly measured and estimated LDL-C.
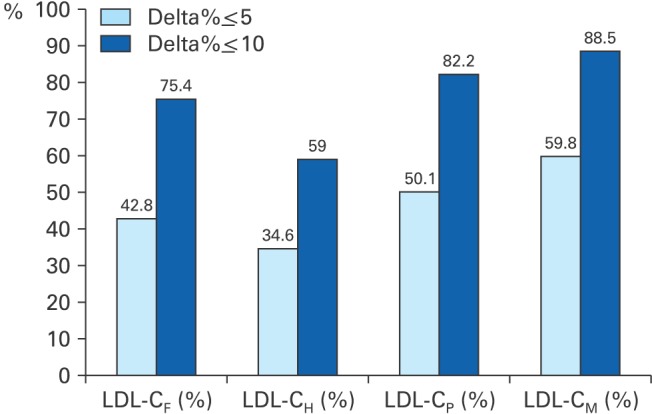
Table 1
Equations for LDL-C concentration estimation

LDL-C, low-density lipoprotein cholesterol; TC, total cholesterol; HDL-C, high-density lipoprotein cholesterol; TG, triglyceride; LDL-CF, LDL-C level estimated by Friedewald equation; LDL-CH, LDL-C level estimated by Hatta equation; LDL-CM, LDL-C level estimated by Martin equation; LDL-CP, LDL-C level estimated by the Puavilai equation.
Table 2
Baseline characteristics of the subjects
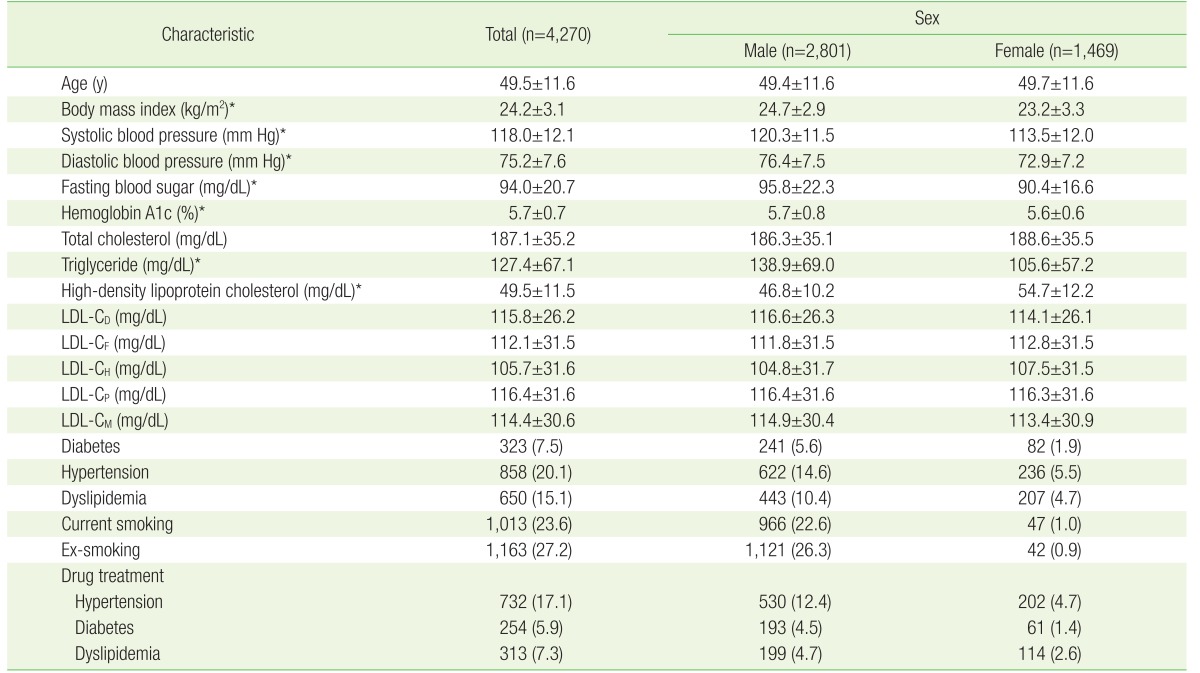
Values are presented as mean±standard deviation or number (%).
LDL-C, low-density lipoprotein cholesterol; LDL-CD, directly measured LDL-C; LDL-CF, LDL-C level estimated by Friedewald equation; LDL-CH, LDL-C level estimated by the Hatta equation; LDL-CM, LDL-C level estimated by the Martin equation; LDL-CP, LDL-C level estimated by the Puavilai equation.
*P-value <0.05 by the Student t-test.
Table 3
Differences between LDL-C estimates by each equations and directly-measured LDL-C

Values are presented as mean±standard deviation.
LDL-C, low-density lipoprotein cholesterol; Diff, absolute value of the difference between a direct measurement and an estimation, |(directly measured LDL-C)-(estimated LDL-C)|; Delta%, percentage difference between directly measured and estimated LDL-C, |(directly measured LDL-C)-(estimated LDL-C)|×100/(directly measured LDL-C); LDL-CF, LDL-C estimated level by Friedewald equation; LDL-CH, LDL-C level estimated by the Hatta equation; LDL-CM, LDL-C level estimated by the Martin equation; LDL-CP, LDL-C level estimated by the Puavilai equation.
*By repeated-measures analysis of variance.
Table 4
Comparison of estimated LDL-C and directly-measured LDL-C by TG levels

Values are presented as mean±standard deviation. The same letters (a ,b, c, d) indicate non-significant differences between groups based on the Scheffe multiple comparison test.
LDL-C, low-density lipoprotein cholesterol; TG, triglyceride; LDL-CD, directly measured LDL-C; LDL-CF, LDL-C level estimated by Friedewald equation; Diff, absolute value of the difference between a direct measurement and an estimation, |(LDL-CD)-(estimated LDL-C)|; Delta%, percentage difference between directly measured and estimated LDL-C, |(LDL-CD)-(estimated LDL-C)|×100/(LDL-CD); LDL-CH, LDL-C level estimated by the Hatta equation; LDL-CM, LDL-C level estimated by the Martin equation; LDL-CP, LDL-C level estimated by the Puavilai equation.
*P-value <0.05 by one-way analysis of variance.
Table 5
Comparison of estimated and directly-measured LDL-C by HDL-C levels
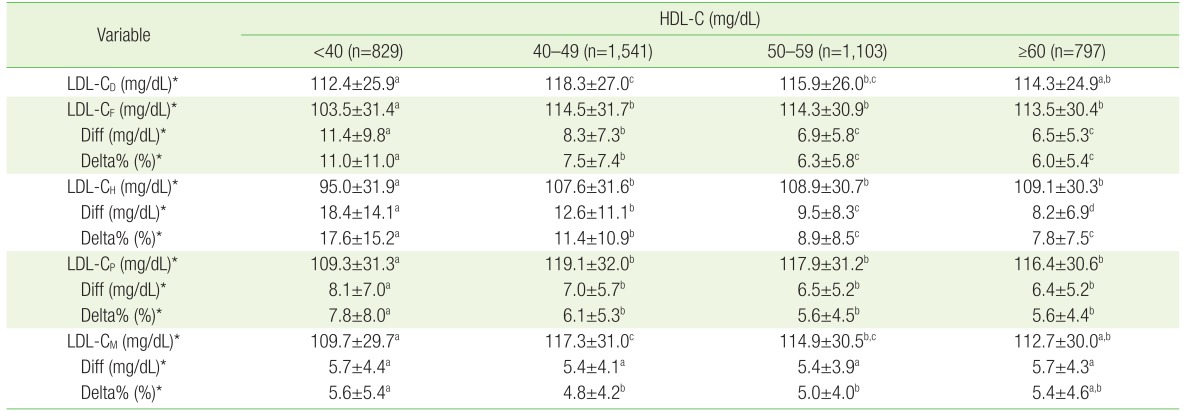
Values are presented as mean±standard deviation. The same letters (a, b, c, d) indicate non-significant differences between groups based on the Scheffe multiple comparison test.
LDL-C, low-density lipoprotein cholesterol; HDL-C, high-density lipoprotein cholesterol; LDL-CD, directly measured LDL-C; Diff, absolute value of the difference between a direct measurement and an estimation, |(LDL-CD)-(estimated LDL-C)|; Delta%, percentage difference between directly measured and estimated LDL-C, |(LDL-CD)-(estimated LDL-C)|×100/(LDL-CD); LDL-CF, LDL-C level estimated by Friedewald equation; LDL-CH, LDL-C level estimated by the Hatta equation; LDL-CM, LDL-C level estimated by the Martin equation; LDL-CP, LDL-C level estimated by the Puavilai equation.
*P-value <0.05 by one-way analysis of variance.
- TOOLS






