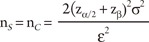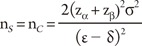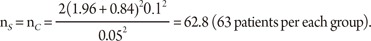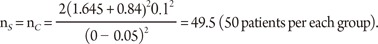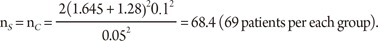In this section, we explain the methods for calculating sample sizes in clinical researches according to various purposes of study, such as equality, non-inferiority, superiority, and equivalence, which appeared in the article titled, "Effects of Korean red ginseng on cardiovascular risks in subjects with metabolic syndrome: a double-blind randomized controlled study", published in July 2012 by Park et al.
1)
Determination of a Sample Size
In most clinical trials, the primary study objective is usually related to the evaluation of the effectiveness and safety of a drug product. For example, it may be of interest to show that the study drug is effective and safe as compared to a placebo. In some cases, it may be of interest to show that the study drug is as effective as, superior to, or equivalent to an active control agent or a standard therapy.
Thus, hypotheses regarding medical or scientific questions of the study drug are usually formulated based on the primary study objectives. The hypotheses are then evaluated using appropriate statistical tests under a valid study design.
2)
A typical approach for demonstration of the efficacy and safety of a study drug under investigation is to test one of the following hypotheses (Here, we assume that the primary study object is the comparing means which is obtained from a two-sample parallel design).
1) Test for equality
where µS and µC are the mean responses for the study and control drugs, respectively.
2) Test for non-inferiority
where µC and µS are the means for the control (standard) and study drugs, respectively, and δ is a difference of clinical importance which is usually called the "non-inferiority margin."
3) Test for superiority
where µS, µC, and δ are defined as in the test for non-inferiority, but in this case, we call δ the "superiority margin."
4) Test for equivalence
where µS, µC, and δ are defined as in the test for non-inferiority, but in this case, we call δ the "equivalence margin."
2. Formulae
For all cases, we further assume that both groups have equal numbers of patients, i.e., nS = nC, the true mean difference between the two groups is ε = µS - µC (>0), and σ2 is a pooled estimate of the variance in both groups.
1) Test for equality
where zα/2 and zβ are the upper (α/2)th quantile and the upper (β)th quantile of the standard normal distribution, respectively.
2) Test for non-inferiority/superiority
where zα and zβ are similarly defined as in the test for equality.
3) Test for equivalence
where zα and zβ/2 are similarly defined as in the test for equality, and we assumed that the true mean difference between the two groups is zero (ε = 0).
3. Examples
Consider the situation that a pharmaceutical company is interested in conducting a clinical trial to compare two cholesterol lowering agents for treatment of patients with coronary heart disease through a parallel design. The primary efficacy parameter is the low density lipoprotein (LDL). In what follows, we will consider the situations where the intended trial is for 1) testing equality of mean responses in LDL, 2) testing non-inferiority or superiority of the study drug as compared to the active control agent, and 3) testing for therapeutic equivalence. All sample size calculations are performed to achieve 80% power (i.e., β = 0.20) at 5% level of significance (i.e., α = 0.05).
1) Test for equality
From the previous studies or a pilot study, we obtain the mean difference between two drugs as 5% in percent change of LDL, which can also be considered as the clinically meaningful difference, and the standard deviation is 10%. Then
2) Test for non-inferiority/superiority
Suppose that the difference of 5% is a difference of clinical importance and the true difference between two groups is zero. Then
3) Test for equivalence
Suppose that the true difference between two groups is zero and the equivalence margin is 5%. Then
Notes
References
- 1. Park BJ, Lee YJ, Lee HR, Jung DH, Na HY, Kim HB, et al. Effects of Korean red ginseng on cardiovascular risks in subjects with metabolic syndrome: a double-blind randomized controlled study. Korean J Fam Med 2012;33:190-196. PMID: 22916320.
- 2. Chow SC, Shao J, Wang H. Sample size calculation in clinical research. 2003. New York: Marcel Dekker Inc..
Citations
Citations to this article as recorded by
