Comments on Statistical Issues in July 2013

Article information

COMPLETE AND QUASI-COMPLETE SEPARATIONS

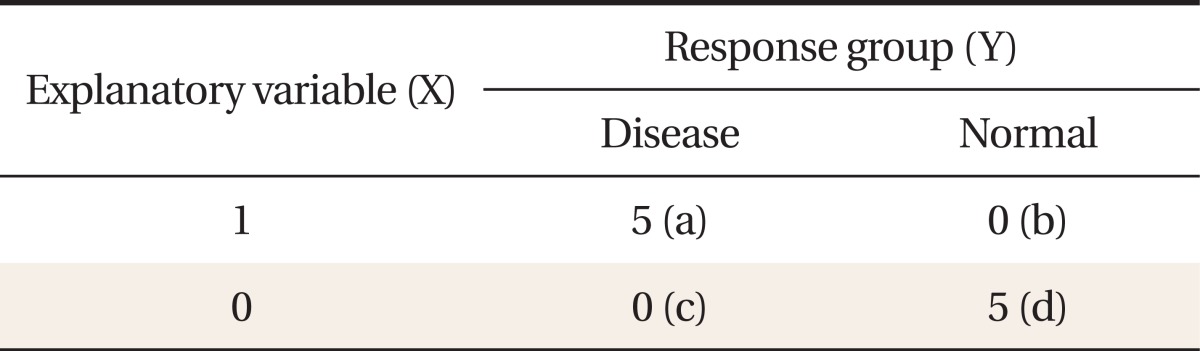
We often confront various numerical problems such as non-convergence in estimating regression coefficients, unreasonably large standard errors, and wide ranges of confidence intervals when analyzing a multiple logistic regression. These problems are caused by certain structures in the data and a lack of appropriate checks in statistical software. We illustrate these data structures in certain simple situations and illustrate what can happen when the logistic regression model is fit to such data. The simplest and thus most obvious situation is when we have a frequency of zero in a contingency table. Consider the following data set (Table 1).

Table 1

A contingency table with a complete separation

The estimated odds ratio using X = 0 as the reference is infinite [OR = (a/b)/(c/d)] = (5/0)/(0/5) = 25/0] since all subjects are completely divided into disease and normal according to the values of X (complete separation). Note that if either (b) or (c) is equal to zero, then the odds ratio is undefined. The standard error of the estimated odds ratio is estimated by the formula,

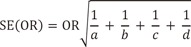
Thus we also obtain an infinite value of standard error for odds

Also note that if any one of the four cell frequencies is equal to zero, then SE(OR) is undefined.

Gart and Zweifel2) suggested improved estimates of OR and SE(OR) which are calculated after adding 0.5 to each cell. According to their suggestion, we obtain OR' = (5.5/0.5)/(0.5/5.5) = 121 and SE(OR') = 252.76.

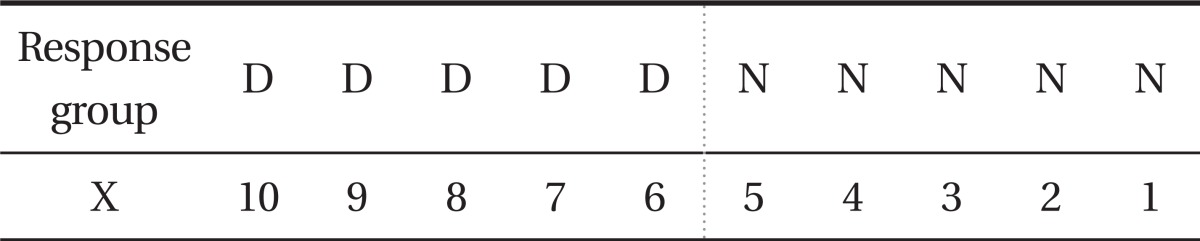
The complete separation can also occur when the values of a continuous explanatory variable are completely divided into both response groups by a certain cut-off as shown in Table 2.

Table 2

Complete separation of a continuous explanatory variable

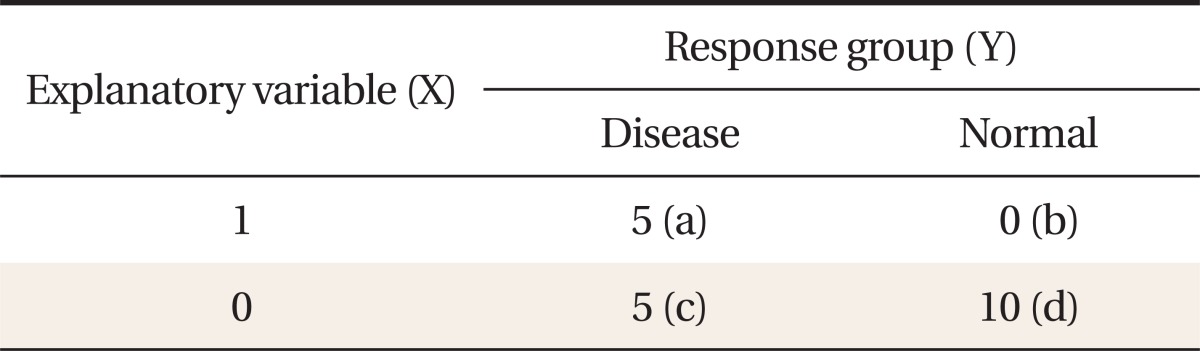
A quasi-complete separation is similar to a complete separation except that there is overlap at a single or a few tied values in both groups. Examples of quasi-complete separations for a discrete and a continuous explanatory variable are presented in Tables 3, 4, respectively.

Table 3

A contingency table with a quasi-complete separation

Table 4

Quasi-complete separation of a continuous explanatory variable

The values of odds ratio and its standard error cannot be estimated unless we apply the suggested method.

SOLUTIONS FOR SEPARATIONS

When a multiple logistic model has too many explanatory variables, we run the risk that the data are too sparse to be able to estimate all the regression coefficients. For example, assume that we have only one binary explanatory variable and forty observations which are distributed evenly to four cells, then each cell has at least ten observations and we do not have numerical problems. However, if we have five binary explanatory variables (sixty-four cells) with the same number of observations, then some cells unavoidably have no observations.

In this case, discarding some obviously unimportant variables with univariate analysis may remedy these problems. The best solution for the numerical problems appears to be the penalized likelihood estimation method which is available in SAS ver. 9.2 (SAS Institute Inc., Cary, NC, USA) with the Firth option in the Logistic procedure.

Article information Continued