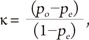In this section, we explain Cohen's kappa coefficient, a measure of agreement, which appeared in the article titled, 'Impact of Clinical Performance Examination on Incoming Interns' Clinical Competency in Differential Diagnosis of Headache', by Park et al.
1) published in March 2014.
KAPPA, A MEASURE OF AGREEMENT
Cohen's kappa coefficient is a statistical measure of interrater agreement or inter-instrument agreement for qualitative (categorical) items. It is generally thought to be a more robust measure than a simple percent agreement calculation since kappa takes into account agreement occurring by chance. A chance-corrected measure originally introduced by Scott,
2) was extended by Cohen
3) and has come to be known as Cohen's kappa. It comes from the notion that the observed cases of agreement include some cases for which the agreement was by chance alone.
Let us assume that there are two raters, who independently rate
n subjects into one of two mutually exclusive and exhaustive nominal categories. Let
pij be the proportion of subjects that are placed in the
i,
jth cell, i.e., assigned to the ith category by the first rater and to the
jth category by the second rater (
i,
j = 1, 2). Also, let
pi+ =
pi1 +
pi2 denote the proportion of subjects placed in the ith row (i.e., the ith category by the first rater), and let
p+j =
p1j +
p2j denote the proportion of subjects placed in the jth column (i.e., the
jth category by the second rater). Then the kappa coefficient is
where po = p11 + p22 is the observed proportion of agreement and pe = p1+p+1 + p2+p+2 is the proportion of agreement expected by chance.
If there is complete agreement, κ = 1. If observed agreement is greater than or equal to chance agreement, κ ≥ 0, and if observed agreement is less than chance agreement, κ < 0. The minimum value of κ depends on the marginal proportions. If they are such that pe = 0.5, then the minimum equals -1. Otherwise, the minimum is between -1 and 0.
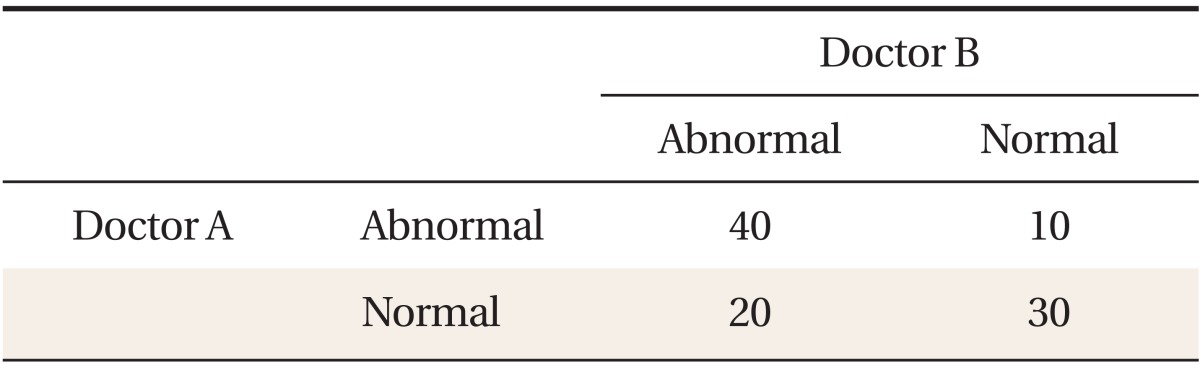
Example. Two doctors independently classified 100 people into one of two diagnostic categories, abnormal/normal as follows (
Table 1).
However, we should not use kappa as a measure of agreement when all raters or devices cannot be treated symmetrically. When one of the sources of ratings may be viewed as superior or a standard, e.g., one rater is senior to the other or one medical device is more precise measuring instrument than the other, kappa may no longer be appropriate.
Notes
References
- 1. Park SM, Song YM, Kim BK, Kim H. Impact of clinical performance examination on incoming interns' clinical competency in differential diagnosis of headache. Korean J Fam Med 2014;35:56-64. PMID: 24724000.
- 2. Scott WA. Reliability of content analysis: the case of nominal scale coding. Public Opin Q 1955;19:321-325.
- 3. Cohen J. A coefficient of agreement for nominal scales. Educ Psychol Meas 1960;20:37-46.
Table 1Diagnoses on n = 100 people by two doctors
Citations
Citations to this article as recorded by
- Comments on Statistical Issues in November 2014
Yong Gyu Park
Korean Journal of Family Medicine.2014; 35(6): 325. CrossRef
