Comments on Statistical Issues in January 2014
Article information
In this section, we suggest some guidelines for reporting multiple linear regression analyses, which appeared in the article titled, "Factors associated with serum levels of carcinoembryonic antigen in healthy non-smokers", by No et al.1) published in November 2013.
GUIDELINES FOR REPORTING MULTIPLE LINEAR REGRESSION ANALYSES
In statistics, the multiple linear regression analysis is an approach to model the relationship between a response variable and several explanatory variables. Typically, a researcher will collect data on several potential explanatory variables, determine which variables are most strongly associated with the response variable, and then incorporate these variables into a mathematical model (a regression equation). The purpose of multiple linear regression analysis, then, is to identify which combination of variables best predicts the response variable.
Here, we suggest some guidelines for reporting a multiple linear regression analysis.
1. State How Each Assumption Was Met and Checked
A statement that the assumptions were verified is all that need be included. The assumptions of a multiple linear regression are as follows: 1) The relationship between each explanatory variable and response variable is linear; 2) The distributions of response variables have equal variances at each value of each explanatory variable; 3) Each response variable value is independent of one another for each value of each explanatory variable; and 4) The response variable has a normal distribution at each value of each explanatory variable. Sometimes, data that violate the assumptions can be adjusted (for example, with data transformation) to meet the required assumptions. If such adjustments are made, it should be noted.
2. Specify How the Final Results Were Derived
Describe the process of selecting the best combination of explanatory variables when the variable selection methods such as stepwise, forward, or backward selection, were used. State whether explanatory variables were assessed for multi-collinearity and tested for interaction.
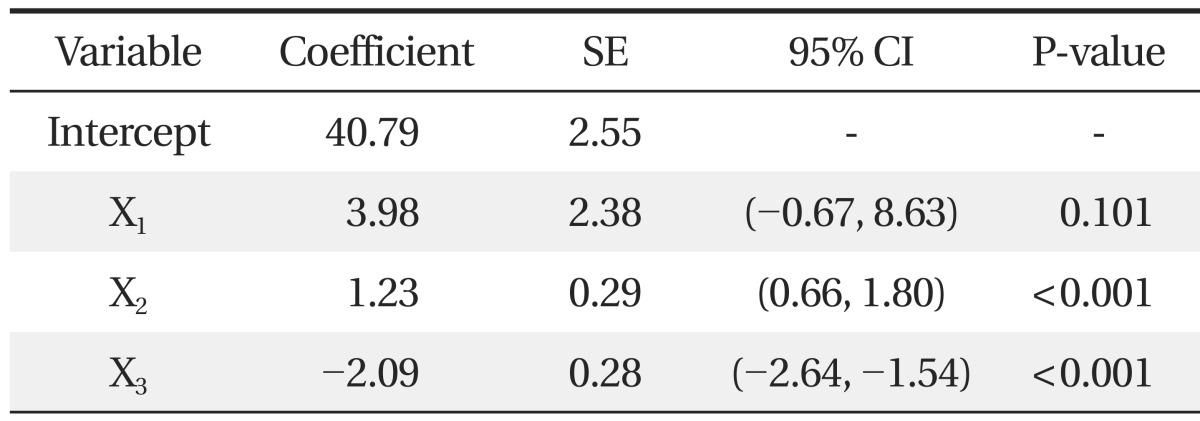
3. Report the Multiple Linear Regression Equation or Summarize the Equation in a Table
An example for reporting a multiple linear regression with three explanatory variables is presented in Table 1.2)
4. Report the Coefficient of Multiple Determination (R2)
The coefficient of multiple determination (R2) indicates how much of the variation in the response variable is explained by the explanatory variables included in the model. An upper-case R should be used.
Notes
No potential conflict of interest relevant to this article was reported.