Martin's Equation as the Most Suitable Method for Estimation of Low-Density Lipoprotein Cholesterol Levels in Korean Adults

Article information

Korean J Fam Med. 2017;38(5):263-269

Publication date (electronic) : 2017 September 22

doi : https://doi.org/10.4082/kjfm.2017.38.5.263

Mijeong Kang , Jongwoo Kim , Seon Yeong Lee , Kyunam Kim , Junehyung Yoon , Hongseok Ki

Department of Family Medicine, Inje University Sanggye Paik Hospital, Seoul, Korea.

Corresponding Author: Jongwoo Kim. Tel: +82-2-950-1150, Fax: +82-2-952-4093, s2700@paik.ac.kr

Received 2016 October 20; Revised 2016 October 24; Accepted 2016 October 24.

Abstract

Background

Friedewald equation is the most widely used method for estimating low-density lipoprotein cholesterol (LDL-C) level. However, due to potential over- or underestimation, many studies have used a modified equation. This study aimed to compare estimates by 4 different equations to directly measured LDL-C concentrations in order to propose the most appropriate method for LDL-C estimation in the Korean population.

Methods

We studied data of 4,350 subjects that included total cholesterol, high-density lipoprotein cholesterol (HDL-C), triglyceride (TG), and LDL-C concentrations that had been measured at one university hospital in Seoul. We investigated 4 equations: LDL-C by Friedewald's original equation (LDL-C_F) and its 3 modifications. Pearson correlation analysis was performed to compare these estimates to the direct measurement.

Results

Pearson correlation analysis revealed a good correlation among all 4 estimated LDL-C values and the directly measured LDL-C value. The Pearson coefficients were 0.951 for LDL-C_F, 0.917 for LDL-C by Hatta equation (LDL-C_H), 0.968 for LDL-C by Puavilai equation (LDL-C_P), and 0.983 for LDL-C by Martin equation (LDL-C_M). Martin equation (LDL-C_M) resulted in the best approximation (mean difference from the direct measurement, 5.5 mg/dL; mean percentage difference from the direct measurement, 5.1%) and the best agreement with the direct measurement (86.1%). LDL-C_P resulted in the second-best approximation (mean difference, 7.0 mg/dL; mean percentage difference, 6.2%; concordance, 82.5%). LDL-C_M was found to be less influenced by TG and HDL-C levels than by LDL-C_F.

Conclusion

Estimates by Martin equation had the best agreement with direct LDL-C concentrations and both Martin and Puavilai equations were superior to Friedewald equation for estimating LDL-C concentrations in Korean adults.

Keywords: Dyslipidemias; Low-Density Lipoprotein Cholesterol; Friedewald Equation; Martin Equation

INTRODUCTION

Based on many studies showing that high serum low-density lipoprotein cholesterol (LDL-C) concentration is the strongest marker of atherosclerosis and an important risk factor for cardiovascular disease (CVD), the US National Cholesterol Education Program Adult Treatment Panel III (NCEP-ATP III) has recommended that serum LDL-C level should be the primary target in dyslipidemia treatment. In addition, dyslipidemia patients should be classified into risk categories according to their LDL-C levels, because a strong positive association between LDL-C and CVD has been well-established.1 2 3 4)

The gold standard for LDL-C measurement is β-quantification using ultracentrifugation, but it is a time-consuming process, relatively expensive, and requires large serum sample volume.5) Thus, instead of measuring LDL-C levels directly, LDL-C concentration is usually estimated with Friedewald equation, using total cholesterol, triglyceride (TG), and high-density lipoprotein cholesterol (HDL-C) concentrations, in primary practice. This equation is known to be valid only in patients whose serum TG concentrations are less than 400 mg/dL.6 7)

Friedewald equation uses the assumptions that very low-density lipoprotein cholesterol (VLDL-C) greatly influences TG levels and that the ratio between TG and VLDL-C is 5; however, the actual ratio varies. Thus, many studies have stated that Friedewald equation tends to either overestimate or underestimate LDL-C in individuals, especially in those with conditions such as diabetes mellitus, alcoholic liver disease, and chronic renal failure who are on dialysis.8 9 10 11)

According to a recent study in Korean populations, Friedewald equation accurately estimated directly measured serum LDL-C concentrations in Korean adults only when the TG concentration was within the range of 36–298 mg/dL.12) It tended to overestimate LDL-C when TG was less than 150 mg/dL and underestimate it when TG was over 150 mg/dL. The use of Friedewald equation led to a 9.1% misclassification rate in those with higher TG levels versus an 8.3% misclassification rate in those with lower TG levels.13) Both overestimation and underestimation can be problematic; overestimating LDL-C leads to prescribing unnecessary medication and underestimating it can delay proper treatment. For this reason, many studies have attempted to modify the equation by changing the TG:VLDL-C ratio. A study conducted by DeLong et al.14) suggested an optimal TG:VLDL-C ratio of 6 instead of 5, using a large sample size of 10,483 individuals, and Puavilai et al.15) confirmed that this equation is more accurate than Friedewald's original equation, with an odds ratio of 2.63. Recently, Martin et al.16) suggested an adjustable novel factor instead of a fixed ratio, using the N-strata-specific median TG:VLDL-C ratio classified by TG and non-cholesterol level, which provided more accurate risk classification without additional costs as compared with Friedewald's original equation. Additionally, Lee et al.17) found that Martin's novel method significantly improved the LDL-C estimation when compared with Friedewald equation in the Korean population.

Thus, we aimed to compare each estimate made using these 4 equations with directly measured LDL-C concentrations in order to propose the most appropriate method for LDL-C estimation without significant error in the Korean population.

METHODS

1. Study Subjects

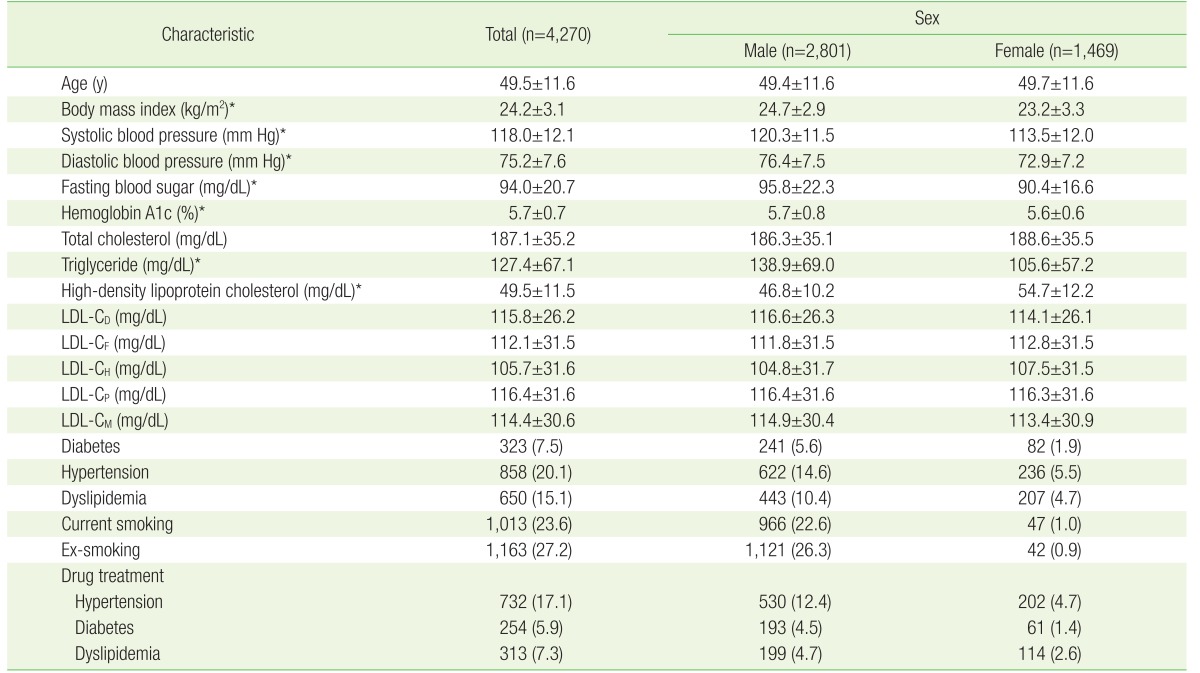
Data were collected retrospectively from 4,350 subjects who had their total cholesterol, HDL-C, TG, and LDL-C levels tested between January 2015 and September 2015 at the Health Promotion Center of Inje University Sanggye Paik Hospital in Seoul, South Korea. We included all patients who were tested during that period, with the exception of 80 subjects who were excluded due to having TG levels over 400 mg/dL. Data of the remaining 4,270 patients (2,801 men and 1,469 women) were analyzed in the current study. This study was approved by the Institutional Review Board of Inje University Sanggye Paik Hospital in Seoul, South Korea (IRB approval No. SGPAIK 2016-05-024).

2. Study Procedure

Body mass index was calculated as weight/height² (kg/m²). Systolic and diastolic blood pressure (mm Hg) was measured by an automated oscillometric blood pressure recorder (Dinamap ProCare 100; GE Healthcare, Milwaukee, WI, USA), with the patients in a seated position after having them relax for five minutes.

Blood samples were obtained from each subject after more than eight hours of fasting. Fasting blood sugar (FBS) level was measured using an enzymatic assay and an automated analyzer (Hitachi Automated Analyzer 7600; Hitachi, Tokyo, Japan). Hemoglobin A1c was measured by high-performance liquid chromatography with the BIO-RAD VARIAN II (BIO-RAD, Hercules, CA, USA). Total cholesterol (Pureauti S CHO-N; Daiichi, Tokyo, Japan), HDL-C (Cholestest N HDL, Daiichi), TG (Pureauto S TG-N, Daiichi), and LDL-C (Cholestest-LDL; Sekisui Medical, Tokyo, Japan) were measured by enzymatic method using the Hitachi Automatic Analyzer 7600 (Hitachi).

To identify the proper TG:VLDL-C ratio, we estimated LDL-C levels by 4 equations shown in Table 1, from the many equations that have been suggested so far.18 19 20 21 22 23 24 25 26) Two of the equations used a different assumption of a TG:VLDL-C ratio, 4 and 6 instead of 5, and the Martin equation used a novel factor as described above. The Martin LDL-C (Martin equation, LDL-C_M) estimate was calculated using an LDL-C calculator instead of the N-strata-specific median TG:VLDL-C ratio classified by TG and non-cholesterol level (http://www.ldlcalculator.com).

Table 1

Equations for LDL-C concentration estimation

The terms used are as follows: “Diff” is defined as the absolute value of the difference between the direct measurement and estimation, and “Delta%” is defined as the percentage difference between directly measured and estimated LDL-C.

To analyze the correlation between directly measured LDL-C and estimated LDL-C, cross-tabulation by Pearson's chi-square was done and directly measured and estimated LDL-C were categorized by the standards of the Korean National Health Insurance Service based on NCEP-ATP III guideline cutoffs of 100, 130, and 160 mg/dL. HDL-C and TG values were categorized by the NCEP-ATP III guideline cutoffs; HDL-C cutoffs were 40, 50, and 60 mg/dL, and TG cutoffs were 100, 150, 200, and 400 mg/dL.

3. Statistical Analysis

Statistical analysis was conducted with SAS ver. 8.11 (SAS Institute Inc., Cary, NC, USA); all data are presented as mean±standard deviation (SD) or proportions. The Student t-test and the chi-square test were used to compare the differences between two groups and Pearson correlation analysis was used to compare correlations between directly measured LDL-C and estimated LDL-C concentrations. A P-value less than 0.05 was considered to be statistically significant. After LDL-C, HDL-C, and TG values were categorized by the NCEP-ATP III guidelines, cross-tabulation by the Pearson chi-square test was used for analysis of the concordance between directly measured and estimated LDL-C. One-way analysis of variance (ANOVA) was performed for multiple comparisons of Diff and Delta% amongst the TG and HDL-C strata.

RESULTS

Table 2 shows the baseline characteristics of the study population overall and by sex. The study group consisted of a total of 4,350 subjects (2,801 men and 1,469 women). The overall age of the study subjects was 49.5±11.6 years and there was no significant difference in age by gender. Men had significantly higher systolic and diastolic blood pressure, FBS, and TG concentration and lower HDL-C concentration than women. Men also had a higher incidence of hypertension, diabetes, dyslipidemia, and current or past smoking history than women.

Table 2

Baseline characteristics of the subjects

Pearson correlation analysis found a good correlation between the 4 estimates of LDL-C and directly measured LDL-C. The Pearson coefficients were LDL-C_F (Friedewald equation, 0.951), LDL-C_H (Hatta equation, 0.917), LDL-C_P (Puavilai equation, 0.968), and LDL-C_M (0.983).

We compared the concordance of the directly measured LDL-C with the estimated LDL-C when classifying LDL-C values by NCEP-ATP III guideline cutoffs of 100, 130, and 160 mg/dL. We labeled the result as being “concordant” if the two values were in the same classification, as an “overestimation” if the estimated value was greater than the direct measurement, or as an “underestimation” if the estimated value was less than the direct measurement. As a result, LDL-C_M resulted in the best concordance with the direct measurement (86.1%) and LDL-C_P resulted in the second-best concordance (82.5%) (Figure 1). LDL-C_F resulted in a concordance of 79.5%, lower than that of LDL-C_M and LDL-C_P. LDL-C_P had the highest rate of overestimation (9.9%); the overestimation using LDL-C_M (5.4%) was similar to that using LDL-C_F (5.8%). Conversely, LDL-C_P had the lowest underestimation rate (7.5%), followed by LDL-C_M (8.6%).

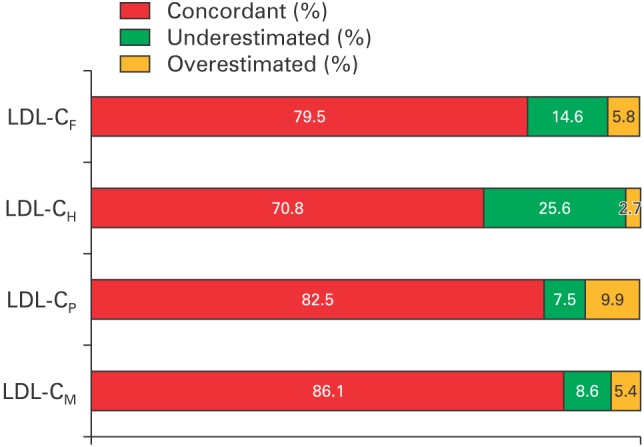
Figure 1

The concordance of estimated LDL-C compared to cutoffs of NCEP-ATP III guideline. LDL-C, low-density lipoprotein cholesterol; NCEP-ATP III, National Cholesterol Education Program Adult Treatment Panel III; LDL-C_F, estimated LDL-C level by Friedewald's equation; LDL-C_H, estimated LDL-C level by Hatta's equation; LDL-C_P, estimated LDL-C level by Puaviali's equation; LDL-C_M, estimated LDL-C level by Martin's equation.

We also compared the proportion of the “Delta%”, the percentage difference between directly measured and estimated LDL-C, which was below 5% and below 10% (Figure 2). According to this result, LDL-C_M is appropriate for the majority of cases, 17% more using Delta% ≤5 and 13.1% more using Delta% ≤10, as compared with LDL-C_F. LDL-C_P was also superior to LDL-C_F (7.3% and 6.8% more, respectively).

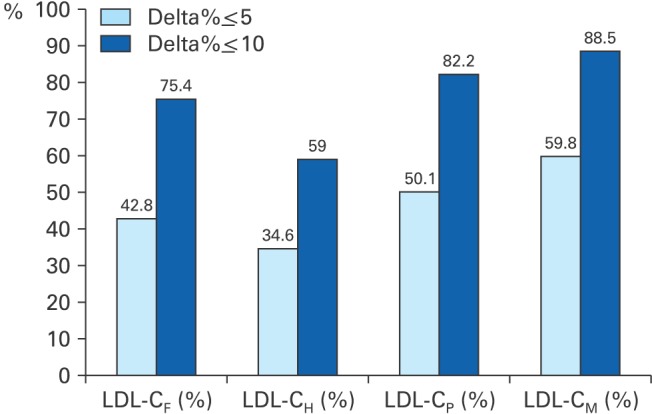
Figure 2

Proportions of percentage difference below 5% and 10% between directly measured and estimated LDL-C. All data are presented as %. LDL-C, low-density lipoprotein cholesterol; LDL-C_F, estimated LDL-C level by Friedewald's equation; LDL-C_H, estimated LDL-C level by Hatta's equation; LDL-C_P, estimated LDL-C level by Puaviali's equation; LDL-C_M, estimated LDL-C level by Martin's equation; Delta%, percentage difference between directly measured and estimated LDL-C.

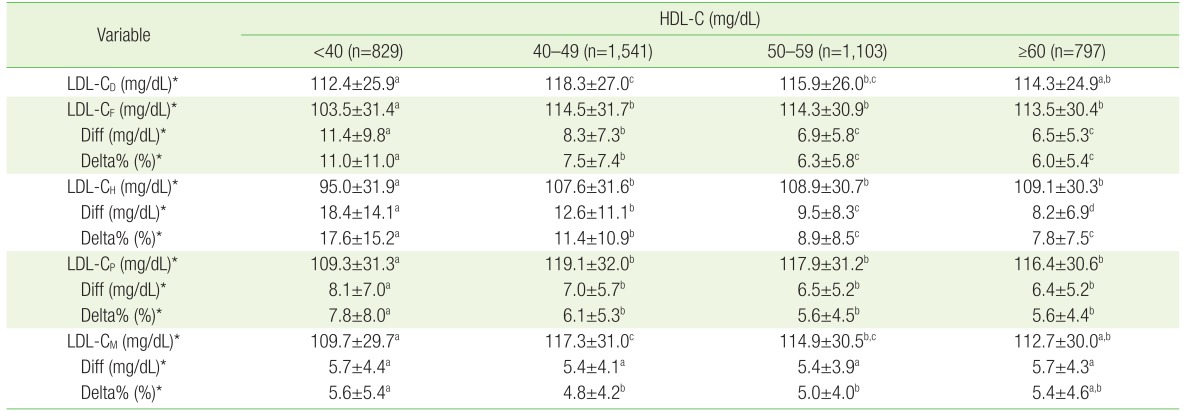
“Diff”, the absolute value of the difference between direct measurement and estimation in terms of mean and SD, is given in Table 3. LDL-C_M was found to produce the best approximate value of the 4 estimations, having a 5.5 mg/dL mean Diff and 5.1% mean Delta%. Meanwhile, LDL-C_F resulted in a mean Diff of 8.2 mg/dL and a mean Delta% of 7.6%. LDL-C_P also produced better results than LDL-C_F, with a mean Diff of 7.0 mg/dL and a mean Delta% of 6.2%.

Table 3

Differences between LDL-C estimates by each equations and directly-measured LDL-C

Because all 4 equations use TG and HDL-C levels as variables, TG and HDL-C are both considered to be the most important independent variables. We compared the means and SDs of LDL estimations by TG and HDL-C strata, using one-way ANOVA (Tables 4, 5). As TG increased, the Diff and Delta% of all 4 equations tended to increase, but LDL-C_M was shown to be less influenced by TG. The Diff and Delta% of LDL-C_F were 5.5 mg/dL and 5.1%, respectively, when the mean TG level was below 100 mg/dL, but they increased drastically as TG increased and reached 18.5 mg/dL and 16.4% when TG was in the range of 200 to 399 mg/dL. The Diff and Delta% of LDL-C_M increased gradually; they were 5.1 mg/dL and 4.9%, respectively, when TG was below 100 mg/dL and 7.1 mg/dL and 6.3% when the TG level was between 200 and 399 mg/dL.

Table 4

Comparison of estimated LDL-C and directly-measured LDL-C by TG levels

Table 5

Comparison of estimated and directly-measured LDL-C by HDL-C levels

Conversely, the Diff and Delta% of all 4 equations tended to decrease as HDL-C increased. The Diff and Delta% of LDL-C_F and LDL-C_M were not significantly different when HDL-C was high, but were significantly different when HDL was below 40 mg/dL.

DISCUSSION

Accurate measurement of LDL-C concentration is very important because it is currently the standard target for dyslipidemia treatment. The gold standard for measuring LDL-C level is β-quantification; however, β-quantitation is not suitable for routine use as it is expensive and time-consuming and requires a large serum sample volume, ultracentrifugation, and expensive instruments.

For these reasons, LDL-C concentration is estimated rather than directly measured in many countries, including Korea, especially in nationwide screening examinations. Many attempts have been made to devise more precise equations by modifying Friedewald's method, but the original Friedewald equation is still the most widely employed method for estimating LDL-C concentration in clinical practice, despite limitations.14 15 16 18 19 20 21 22 23 24 25) Recently, a new method using the N-strata-specific median TG:VLDL-C ratio was developed which uses TG and non-cholesterol level as the adjustable novel factors instead of a fixed ratio of 5.16) This method is reported to significantly improve LDL-C estimation when compared to Friedewald's equation in the Korean population.17)

We focused on the TG:VLDL-C ratio in Friedewald equation and found that there have been several attempts to modify the equation by varying the ratio. The modified equations were suggested for overcoming several limitations of Friedewald's method.26)

We designed this study to compare equations with TG:VLDL-C ratios of 4, 5, and 6 or with a novel factor from the Martin equation. The aim of this study was to compare the accuracy and consistency of these estimated values with directly measured LDL-C and to identify an optimal equation by calculating cutoff values of TG and HDL-C, which are considered the most important variables in all of the equations.

Our results confirmed those of Martin et al.16) and Lee et al.,17) who stated that the Martin equation offers a significant improvement in LDL-C estimation when compared with Friedewald equation. Our results show that the Martin equation is superior to Friedewald equation in that it produces the least difference and best concordance with directly measured LDL-C of the equations studied. Moreover, both the overestimation and underestimation rates are less than those produced by Friedewald equation; the difference is particularly pronounced in the underestimation rate. This is of particular importance because underestimation is generally considered riskier than overestimation, especially when screening the general population, as underestimation can cause delays in initial treatment. We found that the Martin equation is much less influenced by TG or by HDL-C than Friedewald equation.

It is also important that Puavilai equation using a TG:VLDL-C ratio of 6 seems to be superior to Friedewald's equation. It shows less difference and more concordance and produces a lower underestimation rate than Friedewald equation. Therefore, we suggest that this equation needs to be reevaluated in future studies.

This present study has a few limitations. First, the results may not be generalizable to the overall population, as there may be differences in baseline characteristics between our subjects and the general population. Secondly, instead of calculating a novel factor for the Martin equation, we used the calculator that was suggested by the authors, but there is a possibility that the novel factor for the Korean population is different from what Martin reported. Third, because we limited our study subjects to individuals with a TG concentration less than 400 mg/dL, we cannot say that the Martin equation is applicable to individuals with a TG concentration greater than 400 mg/dL. Furthermore, we did not have access to information regarding patients' use of medications that affect lipid profiles, such as oral hypoglycemic agents, lipid lowering agents, and antihypertensive agents.

However, despite these limitations, this study is meaningful because it addresses the use of the Martin equation in a Korean population and compares the results not only to directly measured LDL-C and Friedewald equation but also to various modifications of Friedewald equation. There have been very few studies to date on the use of the Martin equation in Korean populations.

In conclusion, this study showed that the Martin equation is superior to Friedewald equation in Korean adults. It is also notable that the Puavilai equation, which assumes a TG:VLDL-C ratio of 6, produced better results than Friedewald equation in Korean adults.

Notes

CONFLICT OF INTEREST: No potential conflict of interest relevant to this article was reported.

References

1. National Cholesterol Education Program (NCEP) Expert Panel on Detection, Evaluation, and Treatment of High Blood Cholesterol in Adults (Adult Treatment Panel III). Third report of the National Cholesterol Education Program (NCEP) Expert Panel on Detection, Evaluation, and Treatment of High Blood Cholesterol in Adults (Adult Treatment Panel III) final report. Circulation 2002;106:3143–3421. 12485966.

2. Scandinavian Simvastatin Survival Study Group. Randomised trial of cholesterol lowering in 4444 patients with coronary heart disease: the Scandinavian Simvastatin Survival Study (4S). Lancet 1994;344:1383–1389. 7968073.

3. Long-Term Intervention with Pravastatin in Ischaemic Disease (LIPID) Study Group. Prevention of cardiovascular events and death with pravastatin in patients with coronary heart disease and a broad range of initial cholesterol levels. N Engl J Med 1998;339:1349–1357. 9841303.

4. Ridker PM, Stampfer MJ, Rifai N. Novel risk factors for systemic atherosclerosis: a comparison of C-reactive protein, fibrinogen, homocysteine, lipoprotein(a), and standard cholesterol screening as predictors of peripheral arterial disease. JAMA 2001;285:2481–2485. 11368701.

5. Friedewald WT, Levy RI, Fredrickson DS. Estimation of the concentration of low-density lipoprotein cholesterol in plasma, without use of the preparative ultracentrifuge. Clin Chem 1972;18:499–502. 4337382.

6. Lindsey CC, Graham MR, Johnston TP, Kiroff CG, Freshley A. A clinical comparison of calculated versus direct measurement of low-density lipoprotein cholesterol level. Pharmacotherapy 2004;24:167–172. 14998216.

7. Tighe DA, Ockene IS, Reed G, Nicolosi R. Calculated low density lipoprotein cholesterol levels frequently underestimate directly measured low density lipoprotein cholesterol determinations in patients with serum triglyceride levels < or =4.52 mmol/l: an analysis comparing the LipiDirect magnetic LDL assay with the Friedewald calculation. Clin Chim Acta 2006;365:236–242. 16259972.

8. Rubies-Prat J, Reverter JL, Senti M, Pedro-Botet J, Salinas I, Lucas A, et al. Calculated low-density lipoprotein cholesterol should not be used for management of lipoprotein abnormalities in patients with diabetes mellitus. Diabetes Care 1993;16:1081–1086. 8375237.

9. Hirany S, Li D, Jialal I. A more valid measurement of low-density lipoprotein cholesterol in diabetic patients. Am J Med 1997;102:48–53.

10. Johnson R, McNutt P, MacMahon S, Robson R. Use of the Friedewald formula to estimate LDL-cholesterol in patients with chronic renal failure on dialysis. Clin Chem 1997;43:2183–2184. 9365406.

11. Matas C, Cabre M, La Ville A, Prats E, Joven J, Turner PR, et al. Limitations of the Friedewald formula for estimating low-density lipoprotein cholesterol in alcoholics with liver disease. Clin Chem 1994;40:404–406. 8131276.

12. Hwang YC, Ahn HY, Jeong IK, Ahn KJ, Chung HY. Optimal range of triglyceride values to estimate serum low density lipoprotein cholesterol concentration in Korean adults: the Korea National Health and Nutrition Examination Survey, 2009. J Korean Med Sci 2012;27:1530–1535. 23255853.

13. Jang S, Lee J. Friedewald-estimated versus directly measured LDL-cholesterol: KNHANES 2009–2010. J Korea Acad Ind Coop Soc 2015;16:5492–5500.

14. DeLong DM, DeLong ER, Wood PD, Lippel K, Rifkind BM. A comparison of methods for the estimation of plasma low- and very low-density lipoprotein cholesterol: the Lipid Research Clinics Prevalence Study. JAMA 1986;256:2372–2377. 3464768.

15. Puavilai W, Laorugpongse D, Deerochanawong C, Muthapongthavorn N, Srilert P. The accuracy in using modified Friedewald equation to calculate LDL from non-fast triglyceride: a pilot study. J Med Assoc Thai 2009;92:182–187. 19253792.

16. Martin SS, Blaha MJ, Elshazly MB, Toth PP, Kwiterovich PO, Blumenthal RS, et al. Comparison of a novel method vs the Friedewald equation for estimating low-density lipoprotein cholesterol levels from the standard lipid profile. JAMA 2013;310:2061–2068. 24240933.

17. Lee J, Jang S, Son H. Validation of the Martin method for estimating low-density lipoprotein cholesterol levels in Korean adults: findings from the Korea National Health and Nutrition Examination Survey, 2009–2011. PLoS One 2016;11e0148147. 26824910.

18. Hatta Y, Nakajima K. Application of Friedewald’s LDL-cholesterol estimation formula to serum lipids in the Japanese population. Jpn Circ J 1986;50:1191–1200. 3469420.

19. Planella T, Cortes M, Martinez-Bru C, Gonzalez-Sastre F, Ordonez-Llanos J. Calculation of LDL-cholesterol by using apolipoprotein B for classification of nonchylomicronemic dyslipemia. Clin Chem 1997;43:808–815. 9166235.

20. Hattori Y, Suzuki M, Tsushima M, Yoshida M, Tokunaga Y, Wang Y, et al. Development of approximate formula for LDL-chol, LDL-apo B and LDL-chol/LDL-apo B as indices of hyperapobetalipoproteinemia and small dense LDL. Atherosclerosis 1998;138:289–299. 9690912.

21. Wagner AM, Zapico E, Bonet R, Perez A, Ordonez-Llanos J. The effect of VLDL particles on the accuracy of a direct LDL-cholesterol method in type 2 diabetic patients. Clin Biochem 2003;36:177–183. 12726925.

22. Saeidullah M, Rahman M, Khan MH. A simple modification of Friedewald';s equation to calculate low-density lipoprotein cholesterol up to serum triglycerides concentration of 1000 mg/dl. Bangladesh J Med Biochem 2009;2:62–65.

23. Chen Y, Zhang X, Pan B, Jin X, Yao H, Chen B, et al. A modified formula for calculating low-density lipoprotein cholesterol values. Lipids Health Dis 2010;9:52. 20487572.

24. Vujovic A, Kotur-Stevuljevic J, Spasic S, Bujisic N, Martinovic J, Vujovic M, et al. Evaluation of different formulas for LDL-C calculation. Lipids Health Dis 2010;9:27. 20219094.

25. De Cordova CM, de Cordova MM. A new accurate, simple formula for LDL-cholesterol estimation based on directly measured blood lipids from a large cohort. Ann Clin Biochem 2013;50(Pt 1):13–19. 23108766.

26. Nigam PK. Calculated low density lipoprotein-cholesterol: Friedewald's equation versus other modified formulas: calculated LDL-cholesterol. Int J Life Sci Med Res 2014;4:25–31.

Article information Continued

The Korean Academy of Family Medicine

(open-access, http://creativecommons.org/licenses/by-nc/4.0/) :

This is an open-access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.